Launches: Utah: Wales XC Paragliding
Mount Pleasant, Utah, United States · Google
Map
Average Per Year: 2.9 XC Days with 41.9 Flights more than 10 km
Average Monthly Stats
| J Jan | F Feb | M Mar | A Apr | M May | J Jun | J Jul | A Aug | S Sep | O Oct | N Nov | D Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| XC Days | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
|
Avg XC Flights |
0 | 0 | 0 | 0 | 4 | 2 | 1 | 1 | 35 | 0 | 0 | 0 |
| Launch Time | - | - | - | - | 10:52 | 11:22 | 11:20 | 12:08 | 12:48 | - | - | - |
| Yearly Details | ||||||||||||
|
2021 Days
10+ km 25+ km 50+ km |
- - - - | - - - - | - - - - | - - - - | - - - - | 2 10 10 9 | 1 4 4 4 | 0 - - - | 1 9 5 5 | 0 - - - | 0 - - - | 0 - - - |
|
2022 Days
10+ km 25+ km 50+ km |
0 - - - | 0 - - - | 0 - - - | 0 - - - | 1 9 8 4 | 0 - - - | 0 - - - | 2 5 5 5 | 1 3 2 2 | 0 - - - | 0 - - - | 0 - - - |
|
2023 Days
10+ km 25+ km 50+ km |
0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 2 92 91 71 | 0 - - - | 0 - - - | 0 - - - |
|
2024 Days
10+ km 25+ km 50+ km |
0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 0 - - - | 1 46 43 39 | 0 - - - | 0 - - - | 0 - - - |
|
2025 Days
10+ km 25+ km 50+ km |
0 - - - | 0 - - - | 0 - - - | 0 - - - | 1 4 4 2 | 0 - - - | 0 - - - | 0 - - - | 2 24 19 4 | - - - - | - - - - | - - - - |
| Date | Pilot | Pts | Dist |
|---|---|---|---|
| Sep 27, 2025 | scrosier | 32 | 32 km |
| Sep 27, 2025 | zgregy | 14 | 14 km |
| Sep 27, 2025 | laurbor | 13 | 13 km |
| Sep 27, 2025 | StephenGuyette | 15 | 15 km |
| Sep 27, 2025 | kevinkemps | 38 | 38 km |
| Sep 27, 2025 | ewust | 33 | 33 km |
| Sep 27, 2025 | Dr_Jerm | 37 | 37 km |
| Sep 27, 2025 | sclimber | 42 | 42 km |
| Sep 23, 2025 | mmatera | 25 | 18 km |
| Sep 23, 2025 | Carl719 | 20 | 14 km |
| Sep 23, 2025 | mdb | 34 | 34 km |
| Sep 23, 2025 | AndrewTR30 | 57 | 57 km |
| Sep 23, 2025 | jgollan | 45 | 45 km |
| Sep 23, 2025 | AndrewKarnowski | 30 | 30 km |
| Sep 23, 2025 | ramizntoma | 32 | 32 km |
| Sep 23, 2025 | Suntoucher1 | 54 | 54 km |
| Sep 23, 2025 | scrosier | 33 | 33 km |
| Sep 23, 2025 | Jebuterbaugh | 75 | 75 km |
| Sep 23, 2025 | jkellerer | 31 | 31 km |
| Sep 23, 2025 | vmlinux | 46 | 46 km |
| Sep 23, 2025 | scottharding | 76 | 76 km |
| Sep 23, 2025 | Topapilot | 34 | 34 km |
| Sep 23, 2025 | lucassoler333 | 35 | 35 km |
| Sep 23, 2025 | climbhi2 | 35 | 35 km |
| May 9, 2025 | Eskonold | 47 | 47 km |
| May 9, 2025 | mrweiseth | 39 | 39 km |
| May 9, 2025 | ldelacluyse | 112 | 112 km |
| May 9, 2025 | arash.farhang | 194 | 194 km |
| Sep 5, 2024 | mmacarthur | 50 | 50 km |
| Sep 5, 2024 | tom.lanning | 58 | 48 km |
| Sep 5, 2024 | AndriaLea | 14 | 14 km |
| Sep 5, 2024 | skyvine | 90 | 90 km |
| Sep 5, 2024 | cschwie | 95 | 95 km |
| Sep 5, 2024 | flyboy0871 | 95 | 95 km |
| Sep 5, 2024 | WyoWade | 67 | 67 km |
| Sep 5, 2024 | davesnowden | 94 | 94 km |
| Sep 5, 2024 | Mathewjf | 101 | 101 km |
| Sep 5, 2024 | Dodam | 81 | 81 km |
| Sep 5, 2024 | mike.steed | 93 | 93 km |
| Sep 5, 2024 | bwedlock | 95 | 95 km |
| Sep 5, 2024 | aaronrbeck | 94 | 94 km |
| Sep 5, 2024 | BRAVEHEART | 90 | 90 km |
| Sep 5, 2024 | danielegermann | 88 | 88 km |
| Sep 5, 2024 | fandre1535 | 82 | 82 km |
| Sep 5, 2024 | Alicialeggett… | 20 | 20 km |
| Sep 5, 2024 | mdb | 85 | 85 km |
| Sep 5, 2024 | whstites | 93 | 93 km |
| Sep 5, 2024 | stu_frost | 88 | 88 km |
| Sep 5, 2024 | Anna.behrens | 65 | 65 km |
| Sep 5, 2024 | J.Gordon | 89 | 89 km |
| Sep 5, 2024 | reavis | 95 | 95 km |
| Sep 5, 2024 | mtsurveyor | 93 | 93 km |
| Sep 5, 2024 | Themikelester | 93 | 93 km |
| Sep 5, 2024 | alexiaf | 92 | 92 km |
| Sep 5, 2024 | gavin_mcclurg | 92 | 92 km |
| Sep 5, 2024 | cedarwright | 93 | 93 km |
| Sep 5, 2024 | joshcohn | 94 | 94 km |
| Sep 5, 2024 | skymax68 | 97 | 97 km |
| Sep 5, 2024 | martinkubicek | 93 | 93 km |
| Sep 5, 2024 | cmoody6 | 92 | 92 km |
| Sep 5, 2024 | renyijie | 93 | 93 km |
| Sep 5, 2024 | PatrickC | 57 | 47 km |
| Sep 5, 2024 | evan.bouchier | 94 | 94 km |
| Sep 5, 2024 | DougD | 31 | 31 km |
| Sep 5, 2024 | billbelcourt | 93 | 93 km |
| Sep 5, 2024 | guanhai | 92 | 92 km |
| Sep 5, 2024 | vinayshah | 95 | 95 km |
| Sep 5, 2024 | akm130 | 94 | 94 km |
| Sep 5, 2024 | climb1028 | 66 | 66 km |
| Sep 5, 2024 | BDuff | 93 | 93 km |
| Sep 5, 2024 | jwilstein | 96 | 96 km |
| Sep 5, 2024 | DrewWadsworth | 47 | 33 km |
| Sep 5, 2024 | bheinrich | 93 | 93 km |
| Sep 5, 2024 | Itsdavey | 22 | 18 km |
| Sep 15, 2023 | Sealsjeff | 30 | 30 km |
| Sep 15, 2023 | Justin_Caprari | 92 | 92 km |
| Sep 15, 2023 | stu_frost | 39 | 39 km |
| Sep 15, 2023 | samwise19 | 49 | 49 km |
| Sep 15, 2023 | PatrickMattes | 65 | 65 km |
| Sep 15, 2023 | pmilko | 149 | 149 km |
| Sep 15, 2023 | WyoWade | 89 | 89 km |
| Sep 15, 2023 | Jsinason | 29 | 29 km |
| Sep 15, 2023 | Ribz | 63 | 63 km |
| Sep 15, 2023 | danielegermann | 113 | 113 km |
| Sep 15, 2023 | Flynomad | 61 | 61 km |
| Sep 15, 2023 | flymn10k | 73 | 73 km |
| Sep 15, 2023 | vinayshah | 136 | 136 km |
| Sep 15, 2023 | mdb | 45 | 45 km |
| Sep 15, 2023 | alexiaf | 149 | 149 km |
| Sep 15, 2023 | lisaverzella | 75 | 75 km |
| Sep 15, 2023 | Tacoleman1 | 52 | 52 km |
| Sep 15, 2023 | Galenmk | 147 | 147 km |
| Sep 15, 2023 | reavis | 37 | 37 km |
| Sep 15, 2023 | skyvine | 40 | 40 km |
| Sep 15, 2023 | bheinrich | 115 | 115 km |
| Sep 15, 2023 | rdesmond | 147 | 147 km |
| Sep 15, 2023 | GreenGrasshop… | 123 | 123 km |
| Sep 15, 2023 | scottharding | 148 | 148 km |
| Sep 15, 2023 | akm130 | 42 | 42 km |
| Sep 15, 2023 | MitchFriedeman | 45 | 45 km |
| Date | Pilot | Pts | Dist |
|---|---|---|---|
| May 21, 2022 | codymittanck | 361 | 361 km |
| Jun 27, 2021 | billbelcourt | 344 | 344 km |
| Jun 27, 2021 | DrinkMoWater | 337 | 337 km |
| Sep 5, 2022 | tylerburns | 305 | 305 km |
| Jul 6, 2021 | DrinkMoWater | 295 | 295 km |
| Jul 6, 2021 | arash.farhang | 272 | 272 km |
| Aug 7, 2022 | DrinkMoWater | 270 | 270 km |
| Sep 5, 2022 | chukim | 265 | 265 km |
| Jun 28, 2021 | cgalli | 260 | 260 km |
| Jun 28, 2021 | arash.farhang | 250 | 250 km |
| Sep 11, 2023 | jaredscheid | 215 | 153 km |
| May 9, 2025 | arash.farhang | 194 | 194 km |
| Aug 31, 2022 | alecpage | 189 | 189 km |
| Sep 11, 2023 | Galenmk | 188 | 134 km |
| Sep 11, 2023 | mitchriley | 187 | 133 km |
| Jun 27, 2021 | tylerburns | 186 | 186 km |
| Sep 11, 2023 | oneilj411 | 186 | 133 km |
| Sep 11, 2023 | reavis | 185 | 132 km |
| Sep 11, 2023 | Farmer | 185 | 132 km |
| Jun 28, 2021 | Chadclimbrock | 184 | 184 km |
| Sep 11, 2023 | jwilstein | 184 | 132 km |
| Sep 11, 2023 | rdesmond | 184 | 131 km |
| Sep 11, 2023 | bheinrich | 183 | 115 km |
| Sep 11, 2023 | colin911 | 181 | 113 km |
| Sep 11, 2023 | Jlindsay645 | 180 | 112 km |
| Sep 11, 2023 | billbelcourt | 179 | 149 km |
| Sep 11, 2023 | cjessett | 178 | 148 km |
| Sep 11, 2023 | Bowliosis | 177 | 127 km |
| Sep 11, 2023 | climb1028 | 175 | 109 km |
| Sep 11, 2023 | skymax68 | 170 | 141 km |
| Sep 11, 2023 | GreenGrasshop… | 168 | 140 km |
| Sep 11, 2023 | eightate8at8 | 161 | 134 km |
| Sep 11, 2023 | MitchFriedeman | 161 | 134 km |
| Sep 11, 2023 | scottharding | 160 | 134 km |
| Sep 11, 2023 | DrinkMoWater | 160 | 134 km |
| Sep 11, 2023 | vinayshah | 156 | 130 km |
| Aug 31, 2022 | lisaverzella | 153 | 153 km |
| Sep 15, 2023 | colin911 | 152 | 152 km |
| Sep 15, 2023 | Bowliosis | 150 | 150 km |
| Sep 15, 2023 | cmoody6 | 150 | 150 km |
| Sep 15, 2023 | billbelcourt | 150 | 150 km |
| Sep 15, 2023 | alexiaf | 149 | 149 km |
| Sep 15, 2023 | Jackgdiaz | 149 | 149 km |
| Sep 15, 2023 | cjessett | 149 | 149 km |
| Sep 15, 2023 | pmilko | 149 | 149 km |
| Sep 15, 2023 | DavidChen | 148 | 148 km |
| Sep 15, 2023 | DrinkMoWater | 148 | 148 km |
| Sep 15, 2023 | gavin_mcclurg | 148 | 148 km |
| Sep 15, 2023 | evan.bouchier | 148 | 148 km |
| Sep 15, 2023 | scottharding | 148 | 148 km |
| Sep 15, 2023 | skymax68 | 148 | 148 km |
| Sep 15, 2023 | jaredscheid | 147 | 147 km |
| Sep 15, 2023 | tylerburns | 147 | 147 km |
| Sep 15, 2023 | Galenmk | 147 | 147 km |
| Sep 15, 2023 | rdesmond | 147 | 147 km |
| Sep 15, 2023 | pocketpam | 141 | 141 km |
| Sep 15, 2023 | vinayshah | 136 | 136 km |
| Sep 11, 2023 | flymn10k | 127 | 127 km |
| Jun 27, 2021 | lisaverzella | 126 | 126 km |
| Sep 11, 2023 | BDuff | 126 | 126 km |
| Jul 6, 2021 | malansilva | 126 | 126 km |
| Sep 15, 2023 | GreenGrasshop… | 123 | 123 km |
| Sep 15, 2023 | BDuff | 120 | 120 km |
| Sep 15, 2023 | Farmer | 119 | 119 km |
| Sep 11, 2023 | akm130 | 119 | 119 km |
| Sep 15, 2023 | bheinrich | 115 | 115 km |
| Sep 15, 2023 | danielegermann | 113 | 113 km |
| Sep 15, 2023 | rwdunn | 113 | 113 km |
| May 9, 2025 | ldelacluyse | 112 | 112 km |
| Sep 15, 2023 | climb1028 | 105 | 105 km |
| Sep 11, 2023 | JordanNewton | 102 | 102 km |
| Sep 5, 2024 | Mathewjf | 101 | 101 km |
| Sep 5, 2024 | skymax68 | 97 | 97 km |
| Sep 5, 2024 | jwilstein | 96 | 96 km |
| Sep 5, 2024 | bwedlock | 95 | 95 km |
| Sep 5, 2024 | vinayshah | 95 | 95 km |
| Sep 5, 2024 | reavis | 95 | 95 km |
| Sep 5, 2024 | cschwie | 95 | 95 km |
| Sep 5, 2024 | flyboy0871 | 95 | 95 km |
| Sep 5, 2024 | davesnowden | 94 | 94 km |
| Sep 5, 2024 | akm130 | 94 | 94 km |
| Sep 5, 2024 | aaronrbeck | 94 | 94 km |
| Sep 5, 2024 | joshcohn | 94 | 94 km |
| Sep 5, 2024 | evan.bouchier | 94 | 94 km |
| Sep 5, 2024 | mike.steed | 93 | 93 km |
| Sep 5, 2024 | cedarwright | 93 | 93 km |
| Sep 5, 2024 | Themikelester | 93 | 93 km |
| Sep 5, 2024 | BDuff | 93 | 93 km |
| Sep 5, 2024 | bheinrich | 93 | 93 km |
| Sep 5, 2024 | billbelcourt | 93 | 93 km |
| Sep 5, 2024 | renyijie | 93 | 93 km |
| Sep 5, 2024 | whstites | 93 | 93 km |
| Sep 5, 2024 | martinkubicek | 93 | 93 km |
| Sep 5, 2024 | mtsurveyor | 93 | 93 km |
| Sep 5, 2024 | gavin_mcclurg | 92 | 92 km |
| Sep 5, 2024 | guanhai | 92 | 92 km |
| Sep 5, 2024 | cmoody6 | 92 | 92 km |
| Sep 5, 2024 | alexiaf | 92 | 92 km |
| Sep 15, 2023 | Justin_Caprari | 92 | 92 km |
| Sep 30, 2021 | Violeta | 91 | 91 km |
Flight Map Around Wales · View Full Map
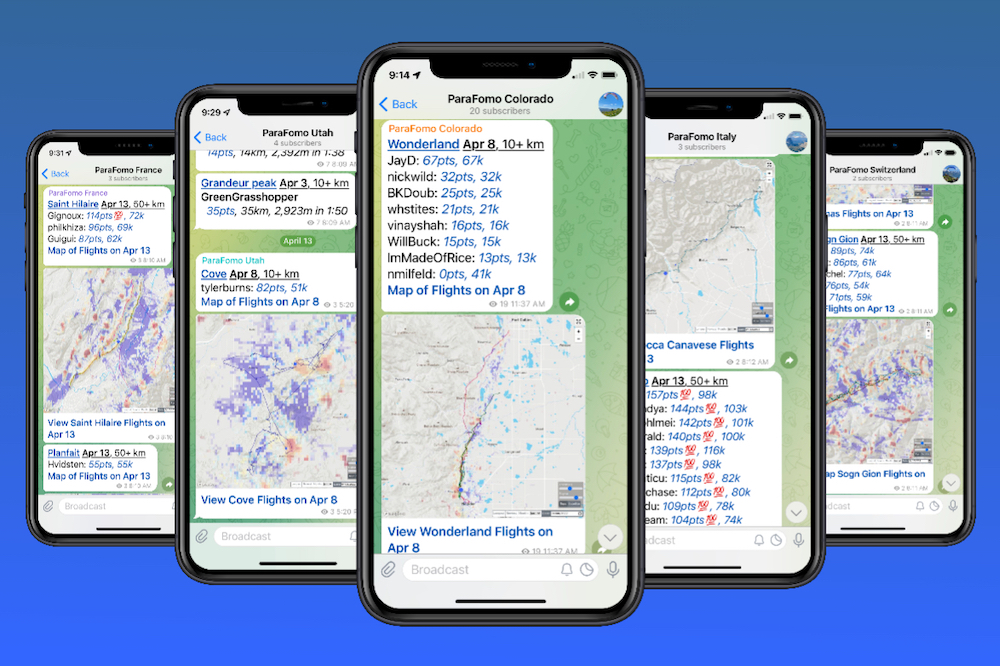
Wales & Utah Flight Reports on Telegram
- New XC flights reported once/day.
- Keep track of who's flying where.